题目描述：给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改链表

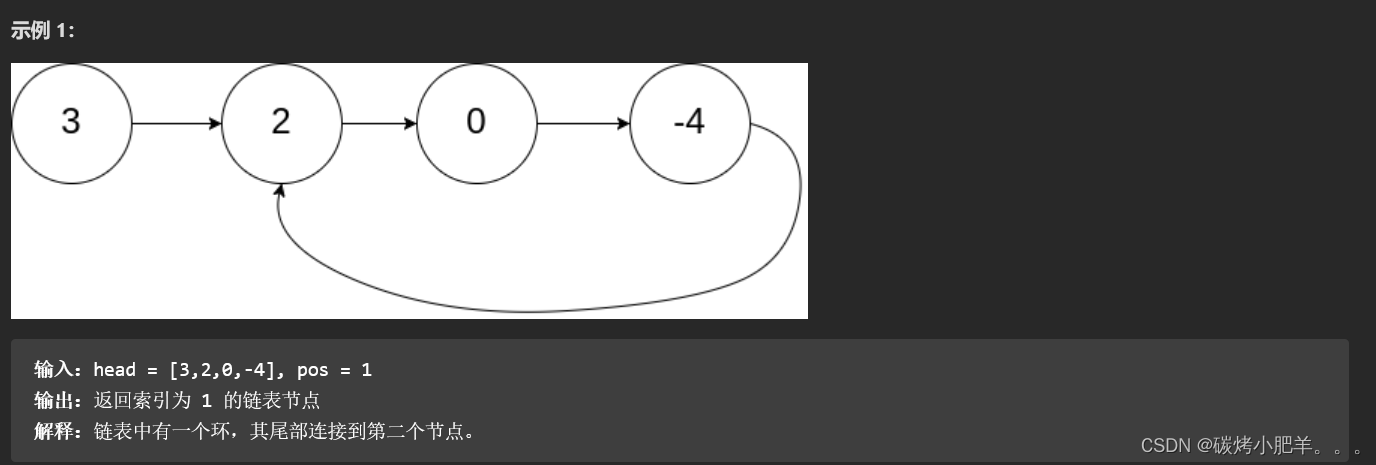
核心思想：快慢指针(slow指针每次移动一步，fast指针每次移动两次) + 寻找数学关系；

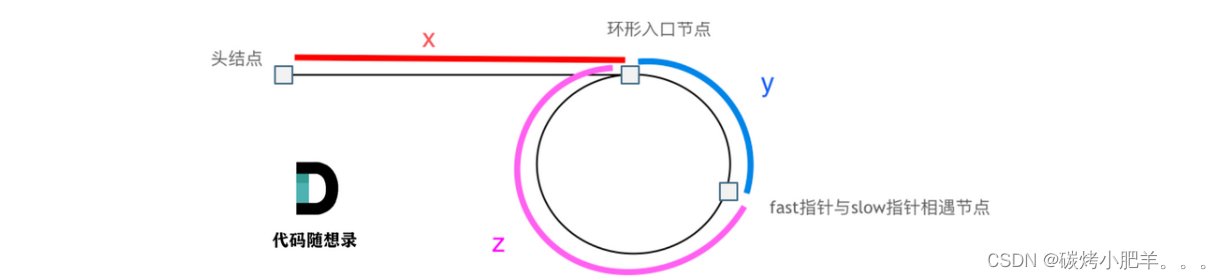
slow 和 fast 指针相遇走的长度：

slow指针运动长度：slow_length = x + y

fast指针运动长度：fast_length = x + y + n（y + z）

因为fast运动是slow运动的2倍，那么fast_length = 2*slow_length;

即 2（x + y） = x + y + n（y + z） ======> x = (n-1)（y + z） + z

当 n为1的时候，公式就化解为 x = z，

这就意味着，从头结点出发一个指针，从相遇节点 也出发一个指针，这两个指针每次只走一个节点， 那么当这两个指针相遇的时候就是 环形入口的节点。

问题：那么 n如果大于1在这里插入代码片是什么情况呢，就是fast指针在环形转n圈之后才遇到 slow指针。

​ 其实这种情况和n为1的时候 效果是一样的，一样可以通过这个方法找到 环形的入口节点，只不过，fast指针在环里 多转了(n-1)圈，然后再遇到slow，相遇点依然是环形的入口节点。

public class Solution {public static ListNode detectCycle(ListNode head) {// 快慢指针ListNode slow = head;ListNode fast = head;// 因为fast每一次移动2步，所以要对fast.next进行判断，如果fast.next为空，那么fast.next.ntxt就会报错while (fast != null && fast.next != null){slow = slow.next;  // 慢指针每一次只移动1次fast = fast.next.next;  // 快指针每一次移动2次if(slow == fast){  // 指针相遇,确定有环while(true){if(head == fast){return fast;}head = head.next;fast = fast.next;}}}return null;}
}