518. 零钱兑换 II

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

示例 1：

输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

示例 2：

输入：amount = 3, coins = [2]
输出：0
解释：只用面额 2 的硬币不能凑成总金额 3 。

示例 3：

输入：amount = 10, coins = [10]
输出：1

提示：

• 1 <= coins.length <= 300
• 1 <= coins[i] <= 5000
• coins 中的所有值 互不相同
• 0 <= amount <= 5000

思路：

此问题属于 0-1背包 的 完全背包 ，解法和 0-1背包类似：

0 - 1背包问题（万能统一代码）

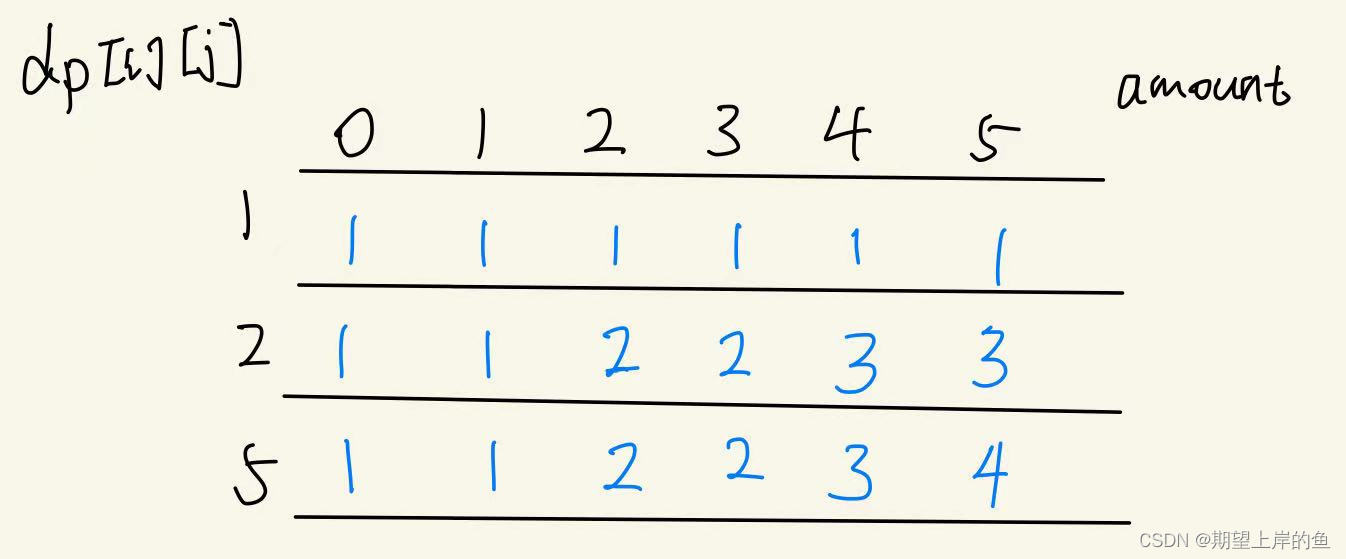
定义一个二维数组dp 存储硬币组合数，其中 dp[i][j] 表示前 i 个硬币 可以凑成总金额 为 j 的 硬币组合数：

• 每种硬币的数量是无限的，所以可以重复使用
• 状态转移方程为：
  dp[i][j]=dp[i−1][j]+dp[i][j−coins[i]]dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]]dp[i][j]=dp[i−1][j]+dp[i][j−coins[i]]

示例1 的dp二维数组为：

观察前 i 个硬币的状态仅与前 i -1 个硬币的状态有关，因此可以优化，将 dp 定义为一维数组，其中 dp[j] 既可以表示 dp[i-1][j] 也可以表示 dp[i ][j - coins[i]]：状态转移方程为：
dp[j]+=dp[j−coins[i]]dp[j] += dp[j - coins[i]]dp[j]+=dp[j−coins[i]]

代码：(Java)

public class Change {public static void main(String[] args) {// TODO Auto-generated method stubint[] coins = {1, 2, 5};int amount = 5;System.out.println(change(amount, coins));}public static int change(int amount, int[] coins) {int[] dp = new int[amount + 1];dp[0] = 1;for(int coin : coins) {for(int i = coin; i <= amount; i++) {dp[i] += dp[i - coin];}}return dp[amount];}
}

运行结果：

复杂度分析：

• 时间复杂度：O(len∗amount)O(len * amount)O(len∗amount), lenlenlen 为数组 coinscoinscoins 的长度，amountamountamount 为要凑成的总金额。
• 空间复杂度：O(amount)O(amount)O(amount) ，需要开辟一个一维数组 dp ， 长度为amount+1amount + 1amount+1 ，amountamountamount 为要凑成的总金额。

322. 零钱兑换 I

注：仅供学习参考 如有不足，欢迎指正！

题目来源：力扣。