[图神经网络]图卷积神经网络--GCN
一、消息传递
由于图具有“变换不变性”(即图的空间结构改变不会影响图的性状),故不能直接将其输入卷积神经网络。一般采用消息传递(Message pass)的方式来处理。
消息传递机制通过局部邻域构建计算图实现,即某个节点的属性由其邻居节点来决定。汇聚这些邻居节点信息的工作由神经网络完成,不用人为干预。其形式如下例:
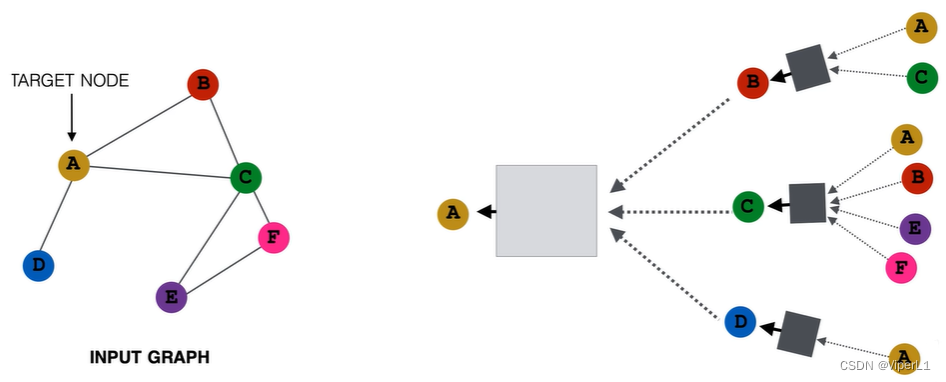
每个节点都可构建属于自己的计算图,计算图可以表征一个其结构、功能和角色。 在计算过程中,每个计算图即为一个单独样本。
需要注意的是,图神经网络的层数并不是神经网络的层数,而是计算图的层数。图神经网络的层数=计算图的层数=图中目标节点的邻居阶数。每一层的节点共享一套计算权重。
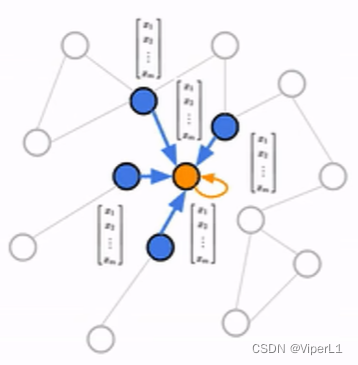
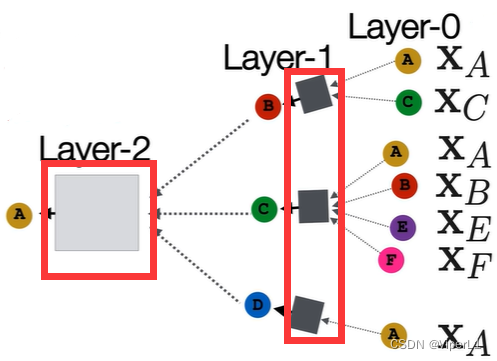
图神经网络的层数 可以视为卷积神经网络中的感受野。若
过大可能导致过平滑(所有节点输出同一张图)
二、图卷积神经网络
1.计算单元
图卷积神经网络基于消息传递方式,一般的计算方法是将邻居节点的属性特征逐元素求平均(与顺序无关,也可以是求最大值/求和),再将这个向量输入到神经元中。

2.数学表示
k+1层 的嵌入是第k层
节点的邻域
计算(邻域
中的节点求和再除以节点
的连接数),其公式可以写作:
式中
为激活函数,
为权重
其中,节点的第0阶属性特征就是其本身:
神经网络输出的嵌入向量为,K为网络的层数
3.矩阵表示
①将k层所有节点的嵌入都记为,
,即下图中矩阵中的一行
②将此矩阵左乘一个邻接矩阵 :
可挑选出节点
的邻域节点(对应上式中的求和过程)
③找到一个矩阵,该矩阵为一个由节点连接数构成的对角矩阵,表现为:

其逆矩阵即为连接数的倒数:
经过上述步骤,式即可表示为
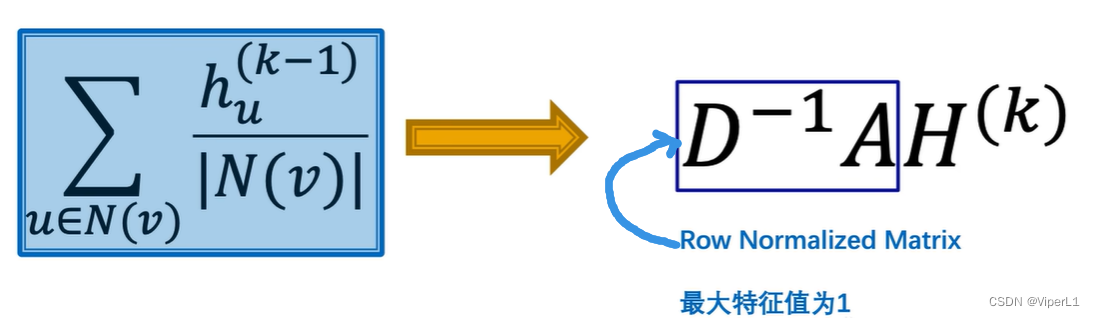
但是这样计算的话,由于造成节点
仅会考虑自己的连接数而忽视对方的连接数(不考虑连接的质量,对全部渠道来得信息强行求平均), 可以将式子改进
-->
,这样得到的结果是一个对称矩阵,既考虑了自身的连接数也考虑了对方的连接数。
可改进后的向量幅值会减小,其特征值值域为(-1,1)。对于这种现象,可以继续对式子进行改进D^{-1}AD^{-1} --> ,这样处理后最大特征值等于1。
最后将此矩阵记为:,在此矩阵中,若两个节点
,
存在连接,则其在矩阵中为
,可以表示其连接权重(其中
和
是节点
和节点
的连接数)

矩阵还可以用来计算拉普拉斯矩阵
则式子可以列为:,该式即可表示一层GCN;其中可学习参数为权重
4.计算图的改进
上述方式(通过相邻节点描述本节点无法反映节点自身的情况),改进方法为:为每个节点加上指向自己的连接。
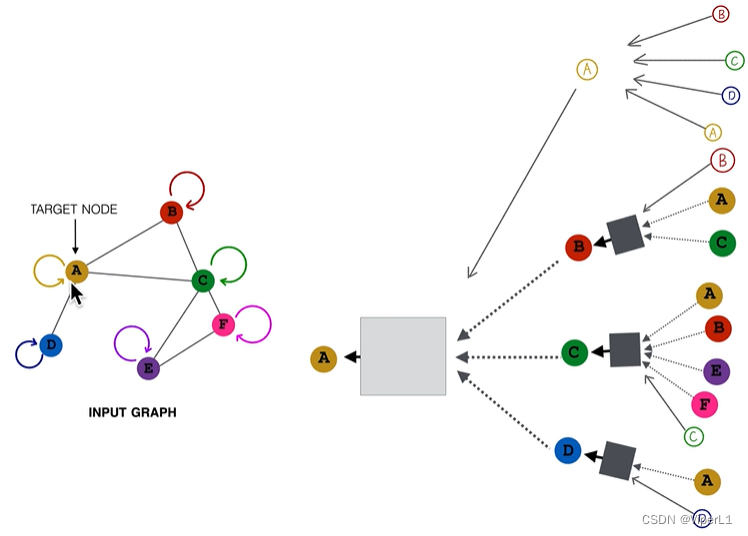
这样改进后,邻接矩阵即变为
(原矩阵加上单位阵,对角线全部为1)
最终神经网络表达式可以写作:
(一个式子包含了原权重矩阵和单位阵)
也可拆分写作:
(前面是对原权重矩阵的变换,后面是对单位矩阵的变换)
进一步改进则可使用两套权重(汇聚节点信息一套,自循环节点信息一套),写作:
且当时,后式变为恒等映射,即为残差连接。
!!!最终的矩阵简化形式为:;其中
三、GCN的训练
1.监督学习
损失函数:,其中f为分类/回归预测头,y为节点标注信息
交叉熵损失函数:

GCN的输入是图结构,输出也是图结构,但输出的图中的节点嵌入了语义信息;输出结构具备:低维、连续、稠密的特点。
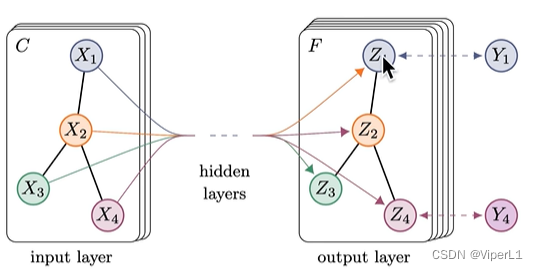
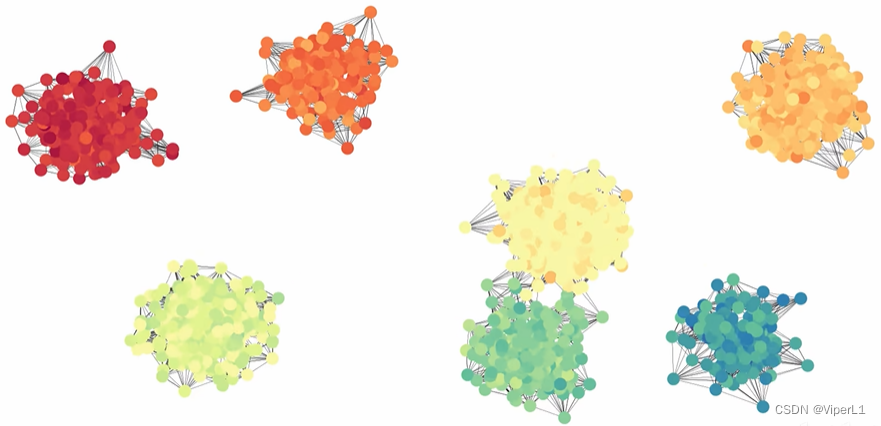
嵌入向量可以输入分类头进行分类,将其映射在二维空间上即可发现不同类别的节点在迭代中被分得越来越开。
 ---->
---->
2.无监督/自检断学习
类似于Deepwalk/Node2vec,利用图自身的连接结构,迭代目的是让图中相连的两个结点嵌入的向量尽可能接近。
损失函数:,当
时表示两个结点
和
相似。
一般采用“编码器--解码器”架构,由编码器将图嵌入到向量,再由解码器计算两个向量的相似度。
四、GCN的优势
相较于传统的基于随机游走的机器学习而言
①GCN所有计算图共享权重,参数量更小
②GCN为归纳式学习,拥有较强的泛化能力(可以泛化到新节点乃至新图--迁移学习)
③利用了节点的属性特征、结构功能角色和标注信息
④拟合学习能力强,得到的嵌入向量质量较高
五、对比CNN、Transformer
1.与CNN对比
CNN可以视为一个2层的GCN,卷积汇总了9个邻居节点和目标节点的信息,其数学式亦可被写成:,CNN可以被视为一个固定邻域、固定顺序的GCN。

但两者之间有以下不同
①CNN不具备变换不变性,打乱像素点的顺序会影响网络的输出。
②GCN的卷积核权重由预定义,不需要学习。而CNN的权重需要学习得来
2.与Transformer对比
Transformer本身是自注意力机制,其训练的目的是让一个序列中的元素之间互相影响。
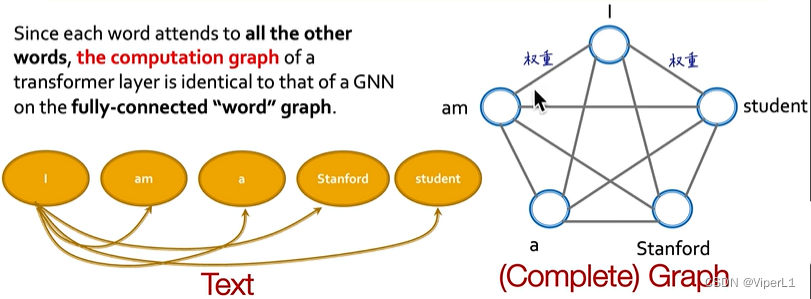
Transformer可以被视为一个全连接词图上的GCN。
