奇异值分解SVD的详细步骤和手算例子_市场资讯

创始人

2025-05-28 16:04:25

0次

奇异值分解（singular value decomposition,SVD）,已经成为矩阵计算中最有用和最有效的工具之一，并且在最小二乘问题、最优化、统计分析、信号与图像处理、系统理论与控制等领域得到广泛应用。

基本原理

按定义来，任何一个矩阵都可以分解成下面的形式：

A=UΣVTA=U \Sigma V^TA=UΣVT

那SVD要求的就是 UUU、 Σ\SigmaΣ、VTV^TVT，其中UUU、VVV是标准正交基（orthonormal），也即
UTU=I,VTV=IU^T U=I, V^T V=I UTU=I,VTV=I

他们的求法如下：

其证明如下：
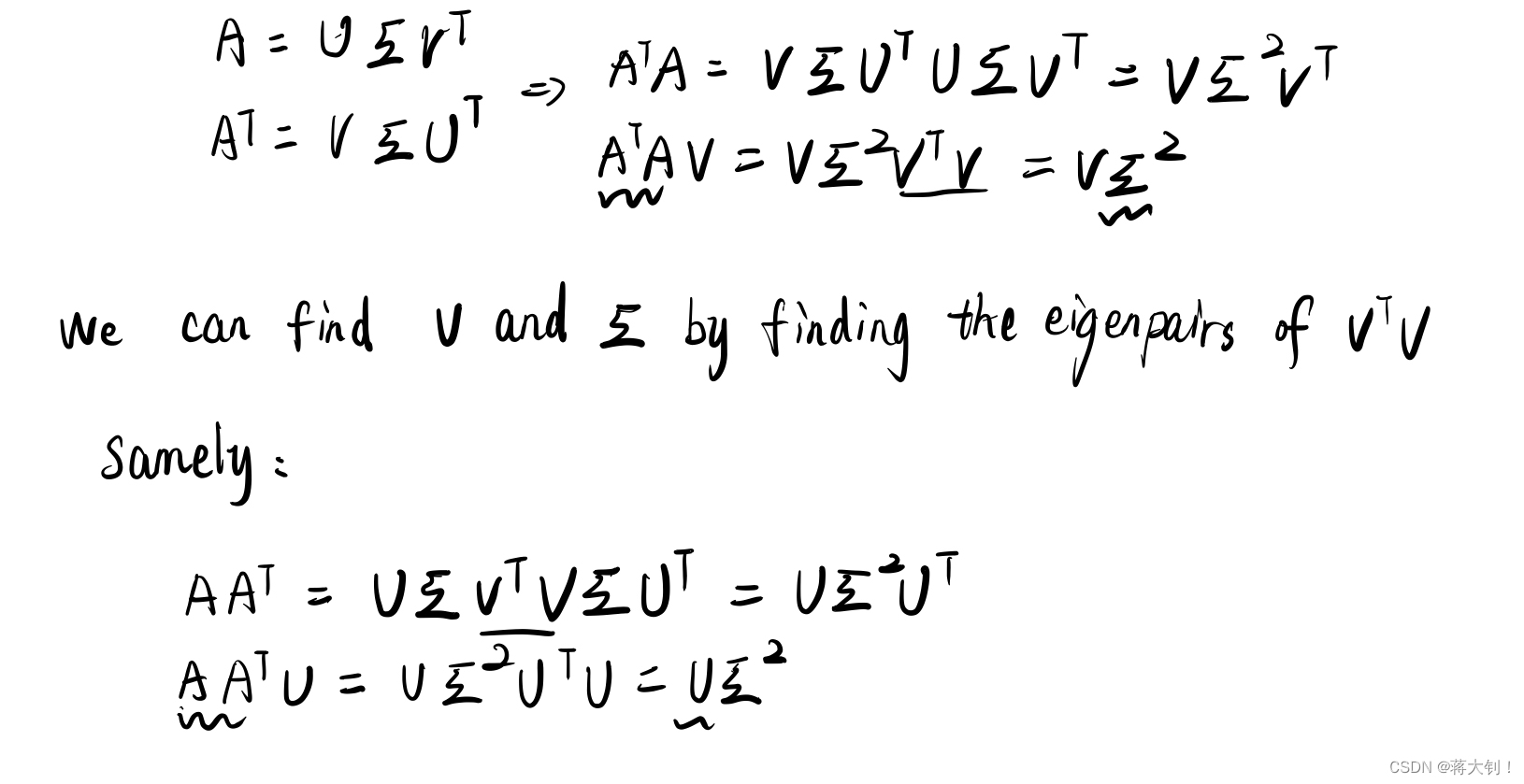
在这里插入图片描述

所以从上面看下来，SVD分解就两步：

举个例子：
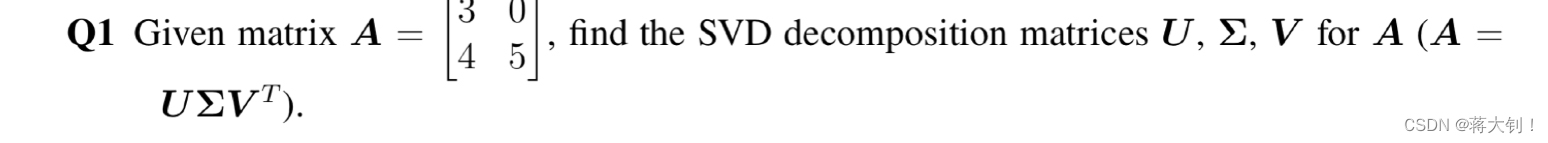
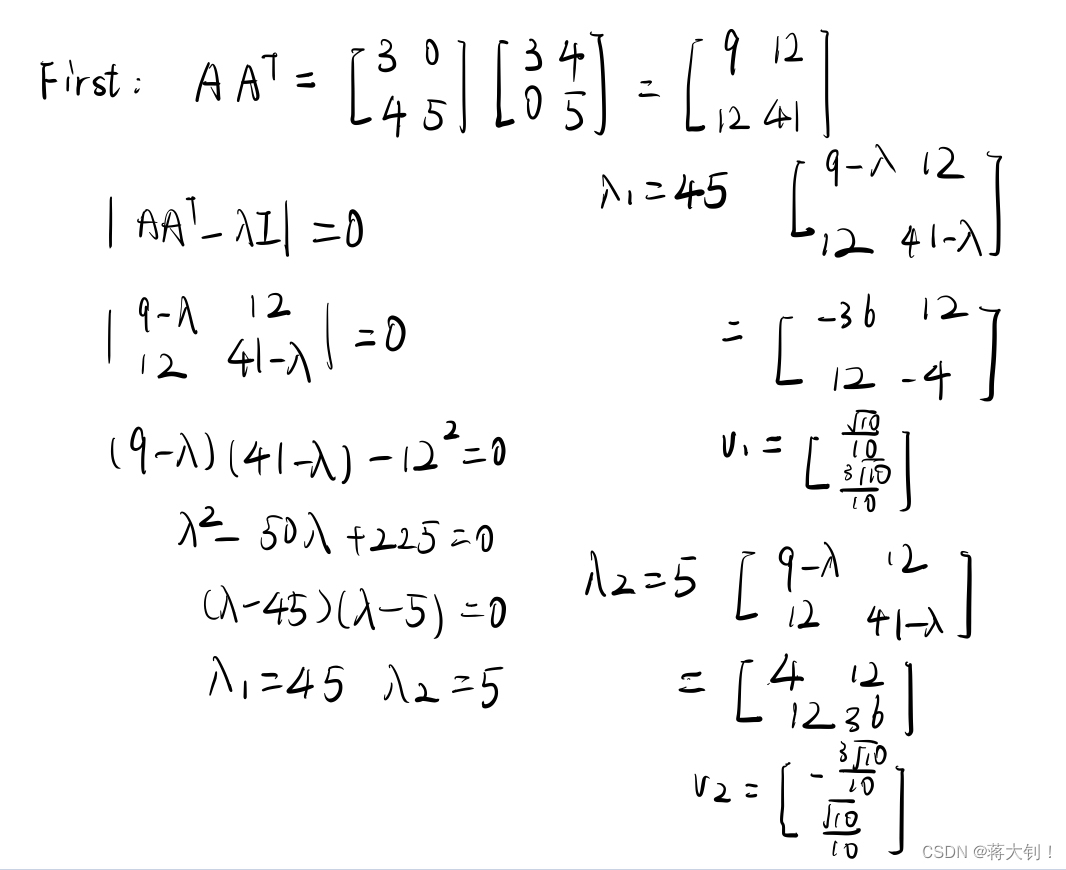
在这里插入图片描述

成都实现境外银行卡“直刷”坐地... 7月28日，成都地铁正式上线银行卡刷卡过闸功能，乘客持银联卡及境外发行的维萨卡（Visa）、万事达卡...

李嘉诚突发！长和一纸公告，坐实... 金融界7月28日消息李嘉诚旗下的长和一纸公告出售港口一事迎来最近进展，坐实内地企业加入交易的传闻。...

坚持绿色发展，华帝荣获《证券之... 7月25日，2025证券之星ESG年度论坛暨第三届ESG新标杆企业奖颁奖盛典在上海盛大举行。作为厨电...

1219亿美元！全球AI领域吸... 人工智能领域正经历着前所未有的资本汇聚浪潮。2025年上半年，全球AI领域吸引风险投资1219亿美元...

美股散户狂欢背后，华尔街空头本... 美股散户持续上演狂欢的同时，华尔街空头正遭受惨痛打击。 S3 Partners数据显示，截至上周四，...

广期所出手，推进光伏组件期货研... 来源：集邦新能源网集邦光储观察获悉，在近期中国光伏行业协会主办的光伏行业2025年上半年发展回顾与...

原创左... 作者︱余在洋与其抱怨环境糟糕，不如弯腰探求“活下来”的创新之道。就像上海这位面馆老板，他用“左手一...

股市必读：金博股份（68859... 截至2025年7月28日收盘，金博股份(688598)报收于27.23元，上涨0.67%，换手率2....

原创高... 8天。2025年春节高速免费通行长达8天，7座及以下小客车全程免单。你是不是也想薅羊毛？想玩个骚操作...

标普500指数屡创新高，大型科... 21世纪经济报道记者舒晓婷北京报道受强劲业绩以及最新贸易动态提振，过去一周美国三大股指集体收涨。...

劲方医药再次冲刺港交所核心产... 劲方医药科技（上海）股份有限公司（以下简称劲方医药）又一次向港交所发起冲刺，计划通过18A规则于主板...

工业硅、多晶硅：7月价格调整，... 【7月28日工业硅期货跌停，多晶硅价格下跌，市场情绪回落致价格大幅调整】7月28日，工业硅期货跌停，...

7.28 十字星出现！指数明天...

大赚超50亿！期货业上半年成绩... 【导读】全国期货公司上半年累计实现净利润50.74亿元见习记者舍梨期货业上半年成绩单揭晓。 7...

赋能产业升级！逸马连锁产业集团... 深圳商报·读创客户端首席记者刘琼 7月28日，由逸马连锁产业集团主办的“百亿连锁蛋糕·百路豪杰共享...

28日纸浆下跌1.72%，最新... 来源：新浪期货新浪期货根据交易所数据，截至7月28日收盘主力合约纸浆2509,涨跌-1.72%,...

美股民热衷“冷门潜力股” 近日，美股市场一甩二季度的阴霾。上周，标准普尔500指数上涨1.5%，至6389点，纳斯达克综合指数...

7月28日江特电机发布公告，股... 证券之星消息，7月28日江特电机发布公告《江特电机:详式权益变动报告书》，其股东王新于2025年2月...

无问芯穹CEO夏立雪：抵达AG... 新浪科技讯 7月28日下午消息，2025年世界人工智能大会期间，无问芯穹联合创始人、CEO夏立雪提出...

5名银行高管，密集履新佛山南都N视频记者从国家金融监督管理总局广东监管局官网获悉，7月22日，佛山监管分局批复了5名银行高管在...