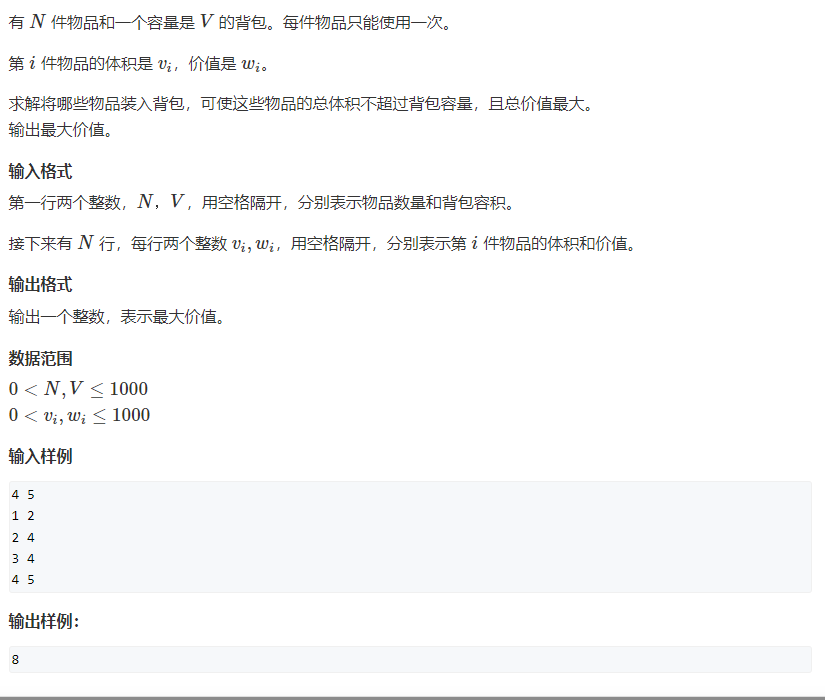
1. 01背包问题

1.1 版本1 二维

（1）状态f[i][j]定义：前 ii 个物品，背包容量 jj 下的最优解（最大价值）：

当前的状态依赖于之前的状态，可以理解为从初始状态f[0][0] = 0开始决策，有 NN 件物品，则需要 NN 次决 策，每一次对第 ii 件物品的决策，状态f[i][j]不断由之前的状态更新而来。
（2）当前背包容量不够（j < v[i]），没得选，因此前 ii 个物品最优解即为前 i−1i−1 个物品最优解：

对应代码：f[i][j] = f[i - 1][j]。
（3）当前背包容量够，可以选，因此需要决策选与不选第 ii 个物品：

选：f[i][j] = f[i - 1][j - v[i]] + w[i]。
不选：f[i][j] = f[i - 1][j] 。
我们的决策是如何取到最大价值，因此以上两种情况取 max() 。

dp数组：所有包括第i个物品且体积不超过j的物品的集合。

核心思想，dp数组的分类处理，是否包含第i件物品，如果不包含

dp[i][j]=dp[i-1][j];

需要保证背包可以装下第i个物品

dp[i][j]=Math.max(dp[i][j],dp[i-1][j-v[i]]+w[i]);

import java.util.*;
public class Main{public static void main(String[] args){Scanner scan = new Scanner(System.in);int N = 1010;int[] v = new int[N];int[] w = new int[N];int[][] f = new int[N][N];int n = scan.nextInt();int m = scan.nextInt();for(int i = 1 ; i <= n ; i ++ ){v[i] = scan.nextInt();w[i] = scan.nextInt();}for(int i = 1 ; i <= n ; i ++ ){for(int j = 0 ; j <= m ; j ++ ){f[i][j] = f[i - 1][j]; // 左边不包含i的方案if(j >= v[i])  f[i][j] = Math.max(f[i][j] , f[i - 1][j - v[i]] + w[i]);//右边包含i的方案，f[i-1][j - v[i]] + w[i]}}System.out.println(f[n][m]);}
}

1.2 版本2 一维

将状态f[i][j]优化到一维f[j]，实际上只需要做一个等价变形。

为什么可以这样变形呢？我们定义的状态f[i][j]可以求得任意合法的i与j最优解，但题目只需要求得最终状态f[n][m]，因此我们只需要一维的空间来更新状态。

（1）状态f[j]定义：NN 件物品，背包容量j下的最优解。

（2）注意枚举背包容量j必须从m开始。

（3）为什么一维情况下枚举背包容量需要逆序？在二维情况下，状态f[i][j]是由上一轮i - 1的状态得来的，f[i][j]与f[i - 1][j]是独立的。而优化到一维后，如果我们还是正序，则有f[较小体积]更新到f[较大体积]，则有可能本应该用第i-1轮的状态却用的是第i轮的状态。

（4）例如，一维状态第i轮对体积为 33 的物品进行决策，则f[7]由f[4]更新而来，这里的f[4]正确应该是f[i - 1][4]，但从小到大枚举j这里的f[4]在第i轮计算却变成了f[i][4]。当逆序枚举背包容量j时，我们求f[7]同样由f[4]更新，但由于是逆序，这里的f[4]还没有在第i轮计算，所以此时实际计算的f[4]仍然是f[i - 1][4]。

（5）简单来说，一维情况正序更新状态f[j]需要用到前面计算的状态已经被「污染」，逆序则不会有这样的问题。

状态转移方程为：f[j] = max(f[j], f[j - v[i]] + w[i] 。

import java.util.*;
public class Main{public static void main(String[] args){Scanner scan = new Scanner(System.in);int N = 1010;int[] v = new int[N];int[] w= new int[N];int[] f = new int[N];int n = scan.nextInt();int m = scan.nextInt();for(int i = 1;i<=n;i++){v[i] = scan.nextInt();w[i] = scan.nextInt();}for(int i = 1; i<=n;i++){for(int j = m;j>=0;j--){if(j >=v[i]) f[j] = Math.max(f[j],f[j-v[i]]+w[i]);}}System.out.println(f[m]);}
}

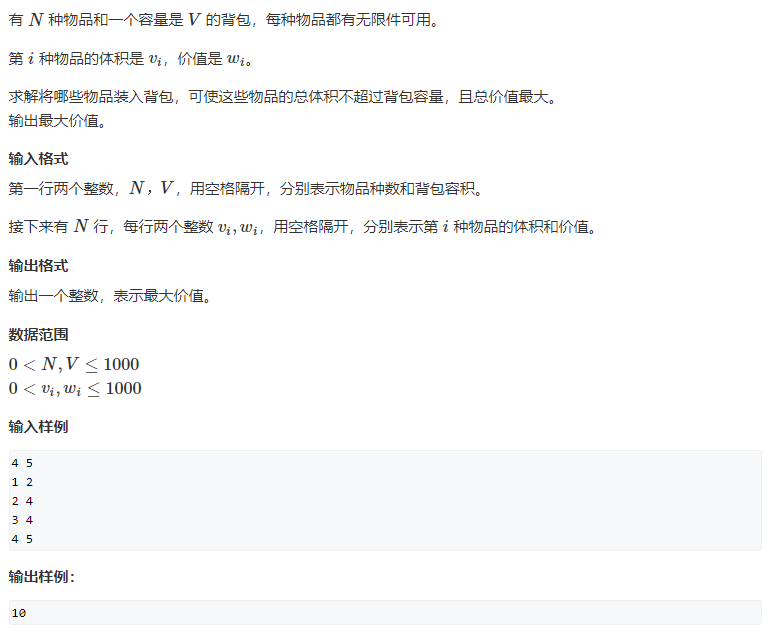
2. 完全背包问题

思路：

同01背包问题。区别在于01背包对于每种物品只有选或不选，这也即「01」的由来。多重背包则对于每种物品可以多次选择。

2.1 二维朴素写法

import java.util.*;
public class Main{public static void main(String[] args){int N = 1010;int[] v= new int[N];int[] w =new int[N];int[][] f = new int[N][N];Scanner scan = new Scanner(System.in);int n = scan.nextInt();int m = scan.nextInt();for(int i = 1; i <= n ;i++){v[i] = scan.nextInt();w[i] = scan.nextInt();}for(int i = 1; i <=n;i++){for(int j = 0;j<=m;j++){f[i][j] = f[i-1][j];if(j >= v[i]) f[i][j] = Math.max(f[i][j],f[i][j-v[i]]+w[i]);}}System.out.println(f[n][m]);}
}

2.2 一维优化版

这里对比01背包问题，注意下标，我们可以发现

if(j >= v[i]) dp[i][j]=Math.max(dp[i][j],dp[i-1][j-v[i]]+w[i]);//01背包
if(j >= v[i]) f[i][j] = Math.max(f[i][j],f[i][j-v[i]]+w[i]);//完全背包

仅仅是f[i]和dp[i-1]的区别，所以对应一维优化

import java.util.*;
public class Main{public static void main(String[] args){Scanner scan = new Scanner(System.in);int N = 1010;int[] v = new int[N];int[] w = new int[N];int[] f = new int[N];int n = scan.nextInt();int m = scan.nextInt();for(int i = 1 ; i <= n ; i ++ ){v[i] = scan.nextInt();w[i] = scan.nextInt();}for(int i = 1 ; i <= n ; i ++ ){for(int j = m ; j >= v[i] ; j -- ){f[j] = Math.max(f[j] , f[j - v[i]] + w[i]);}}}System.out.println(f[m]);}
}

3. 多重背包问题

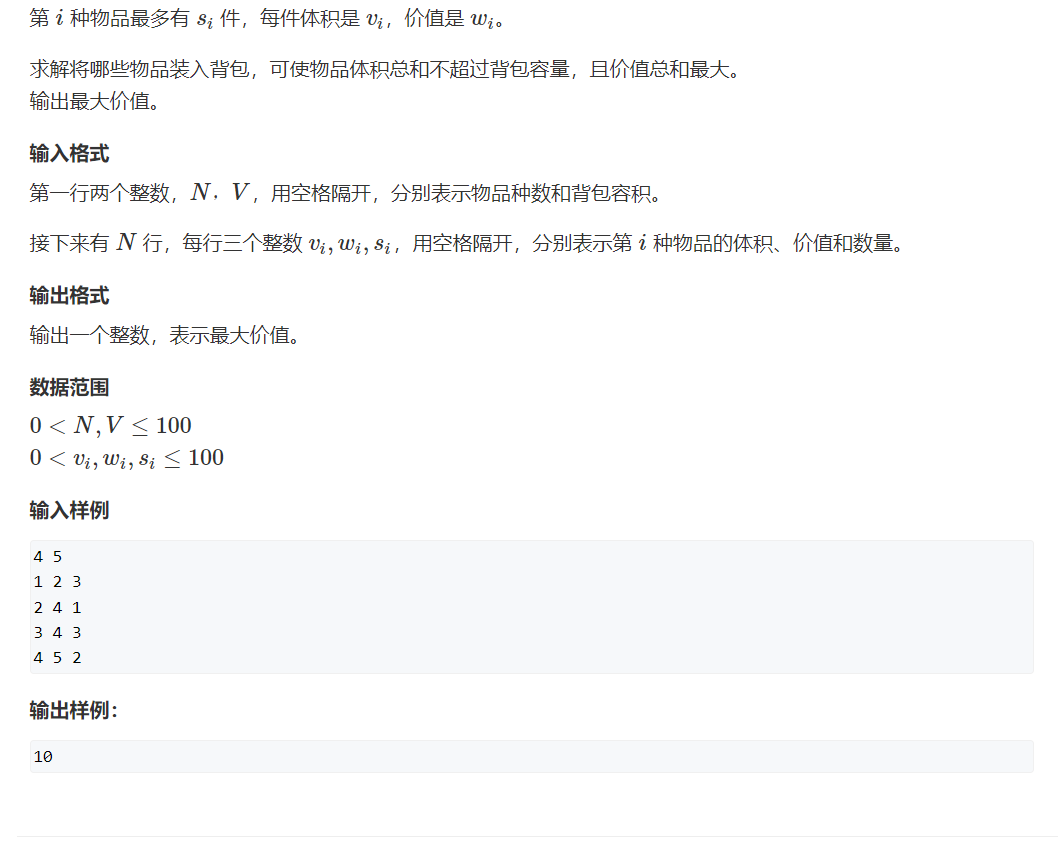
分析

当 si=1 时，相当于01背包中的一件物品
当 si>1 时，相当于01背包中的多个一件物品
故我们可以死拆(把多重背包拆成01背包)

直接枚举第i件物品的选择数，满足总体积不超过j即可

朴素解法

import java.util.*;
public class Main{public static void main(String[] args){Scanner scan = new Scanner(System.in);int N = 110;int[] v = new int[N],w = new int[N],s = new int[N];int[][] f = new int[N][N];int n = scan.nextInt();int m = scan.nextInt();for(int i = 1 ; i <= n ; i ++ ){v[i] = scan.nextInt();w[i] = scan.nextInt();s[i] = scan.nextInt();}for(int i = 1 ; i <= n ; i ++ )for(int j = 0 ; j <= m ; j ++ )for(int k = 0 ; k <= s[i] && k * v[i] <= j; k ++ )f[i][j] = Math.max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);System.out.println(f[n][m]);}
}

4. 分组背包问题

分析：

朴素解法

import java.util.*;
public class Main{public static void main(String[] ags){Scanner scan = new Scanner(System.in);int N = 110;int[][] v = new int[N][N];int[][] w = new int[N][N];int[] s = new int[N];int[] f = new int[N];int n = scan.nextInt();int m = scan.nextInt();for(int i = 1 ; i <= n ; i ++ ){s[i] = scan.nextInt();for(int j = 1 ; j <= s[i] ; j ++ ){v[i][j] = scan.nextInt();w[i][j] = scan.nextInt();}}for(int i = 1 ; i <= n ; i ++ ){for(int j = m ; j >= 0 ; j -- ){for(int k = 0; k <= s[i] ; k ++ ){if(j >= v[i][k])  f[j] = Math.max(f[j], f[j - v[i][k]] + w[i][k]);}}}System.out.println(f[m]);}
}

           for(int k = 0; k <= s[i] ; k ++ ){if(j >= v[i][k])  f[j] = Math.max(f[j], f[j - v[i][k]] + w[i][k]);}}}System.out.println(f[m]);
}

}