一、二叉搜索树的概念

普通的二叉树其实并没有太多的意义。但是通过二叉树可以得到一个延伸的概念，即二叉搜索树。二叉搜索树又称二叉排序树，它具有以下性质：

（1）若它的左子树不为空，则左子树上所有节点的值都小于根节点的值

（2）若它的右子树不为空，则右子树上所有节点的值都大于根节点的值

（3）它的左右子树也分别为二叉搜索树

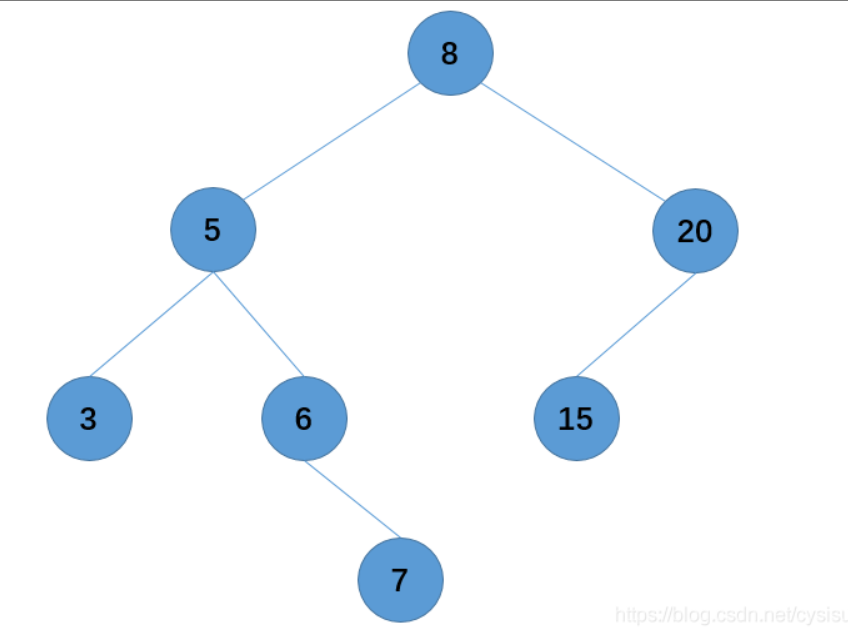
上图就是一个二叉搜索树。可以看到，在上面的二叉树中，它所有的左节点都必然小于它的根节点，而右节点的值则必然大于它的根节点。

1.搜索

从名字上看就可以知道，这种树的主要作用就是用于搜索和排序。在以前学的普通二叉树中，如果想查找一个值，只能使用暴力查找的方式逐个节点的查找，时间复杂度为O（N），效率很低。但是如果使用二叉搜索树，因为其左子节点必然小于根节点和右子节点必然大于根节点的特性，在这上面查找一个数据的时间复杂度就为O（logN），效率非常高。

但是一个二叉搜索树要满足O（logN）的时间复杂度，其实是有一定条件的，就是它的左右节点的层数也趋于平衡，即趋于相等。因为二叉搜素树叶可能出现所有节点都在一边的情况：

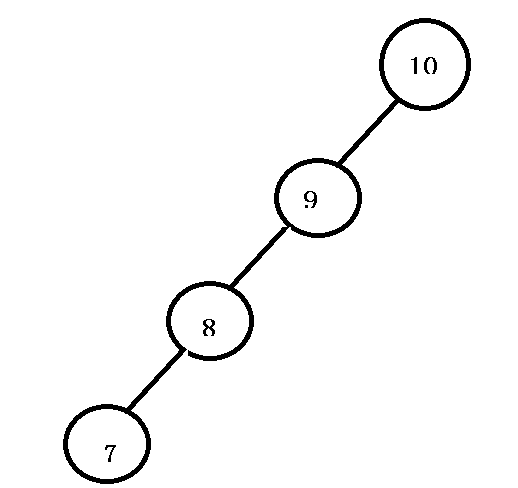
上图中也是一个二叉搜索树，但是它的时间复杂度就是O（N）。因此二叉搜索树在这种极端情况下的查找效率也是很低的。为了解决这个问题，在后面会有一个平衡二叉搜索树，它的左右节点的层数就是趋于相等的，查找效率非常高，这里就先不过多讲解。

1. 排序

二叉搜索树又叫二叉排序树。这就说明，二叉搜索树不仅能用来搜索数据，也能用来排序数据。在二叉搜索树中，如果使用“中序遍历”的方法，就可以将数据按照从小到大的顺序依次取出。

二、二叉搜索树的模拟实现

二叉搜索树的概念很简单。了解了概念后，就可以尝试模拟实现一个二叉搜索树了。

模拟实现代码：

#pragma once
#include
using namespace std;template
struct BSTreeNode
{BSTreeNode(const K& val): _val(val), _right(nullptr), _left(nullptr){}BSTreeNode* _left;BSTreeNode* _right;K _val;
};template
class BSTree
{typedef BSTreeNode Node;
public:BSTree()//构造函数:_root(nullptr){};~BSTree()//析构函数{destory(_root);_root = nullptr;}BSTree(const BSTree& t)//拷贝构造{_root = copy(t._root);}BSTree& operator=(BSTree t)//运算符=重载{swap(_root, t._root);return *this;}bool insert(const K& val)//插入函数{if (_root == nullptr)//为空就是还没有根节点，创建根节点后反悔{_root = new Node(val);return true;}Node* parent = nullptr;//表示cur的父节点，用于在cur找到插入位置时链接Node* cur = _root;while (cur)//找到比val值小{if (val < cur->_val){parent = cur;cur = cur->_left;}else if (val > cur->_val){parent = cur;cur = cur->_right;}elsereturn false;//当插入的值与某个节点的值相等时，返回false结束}cur = new Node(val);//出来后说明cur到了某个节点的空节点处，创建新节点赋值if (val < parent->_val)//将创建出来的新节点与树连接parent->_left = cur;elseparent->_right = cur;return true;}bool find(const K& val)//查找函数{Node* cur = _root;while (cur){if (val < cur->_val)cur = cur->_left;else if (val > cur->_val)cur = cur->_right;elsereturn true;}return false;}bool erase(const K& val)//删除函数{Node* parent = nullptr;Node* cur = _root;while (cur){if (val < cur->_val){parent = cur;cur = cur->_left;}else if (val > cur->_val){parent = cur;cur = cur->_right;}else{if (cur->_left == nullptr)//要删除的节点左为空{if (cur == _root)//要删除的节点为根节点{_root = cur->_right;}else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;}else if (cur->_right == nullptr)//要删除的节点右为空{if (cur == _root)//要删除的节点为根节点{_root = cur->_left;}else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;}else//要删除的节点两边都不为空{Node* min_parent = cur;Node* min_right = cur->_right;while (min_right->_left != nullptr)//找到要删除节点的右子树最小左节点，然后交换值，再删除掉右子树最小左节点{min_parent = min_right;min_right = min_right->_left;}cur->_val = min_right->_val;if (min_parent == cur)//当要交换的节点就是cur的时候min_parent->_right = min_right->_right;elsemin_parent->_left = min_right->_right;delete min_right;}return true;}}return false;}bool insertR(const K& val)//插入的递归版本{return _insertR(_root, val);}bool eraseR(const K& val)//删除的递归版本{return _eraseR(_root, val);}void InOrder()//给_InOrder()函数套一层接口，使得在不暴露函数实现和成员变量的情况下实现调用{_InOrder(_root);cout << endl;}bool findR(const K& val)//查找的递归版本{return _findR(_root, val);}private:bool _insertR(Node*& root, const K& val)//插入的递归版本。此处的引用就是用于替代父节点。因为在递归调用中，它传{                                        //过来的是父节点的root->_left/_right，用引用传的就是别名，直接修改会改变if (root == nullptr)                //树中对应位置的数据，而不是像传拷贝仅仅传值那样无法链接{root = new Node(val);return true;}if (val < root->_val)return _insertR(root->_left, val);else if (val > root->_val)return _insertR(root->_right, val);elsereturn false;}bool _eraseR(Node*& root, const K& val)//删除的递归版本{if (root == nullptr)return false;if (val < root->_val)return _eraseR(root->_left, val);else if (val > root->_val)return _eraseR(root->_right, val);else{Node* del = root;if (root->_left == nullptr)root = root->_right;else if (root->_right == nullptr)root = root->_left;else{Node* min_right = root->_right;while (min_right->_left){min_right = min_right->_left;}swap(min_right->_val, root->_val);return _eraseR(root->_right, val);}delete del;return true;}}void _InOrder(const Node* root)//中序遍历{if (root == nullptr)return;_InOrder(root->_left);cout << root->_val << " ";_InOrder(root->_right);}bool _findR(Node* root, const K& val)//查找的递归版本{if (root == nullptr)return false;if (val < root->_val)return _findR(root->_left, val);else if (val > root->_val)return _findR(root->_right, val);elsereturn true;}Node* copy(Node* root)//提供给拷贝构造函数以进行拷贝构造{if (root == nullptr)return root;Node* new_root = new Node(root->_val);new_root->_left = copy(root->_left);new_root->_right = copy(root->_right);return new_root;}void destory(Node* root)//提供给析构函数调用进行析构{if (root == nullptr)return;destory(root->_left);destory(root->_right);delete root;    }private:Node* _root = nullptr;//给参数加上缺省值
};

二叉搜索树的模拟实现其实也是很简单的。上面的代码中将插入、删除、查找的函数都写了递归的形式。二叉搜索树主要的难点在于删除上。

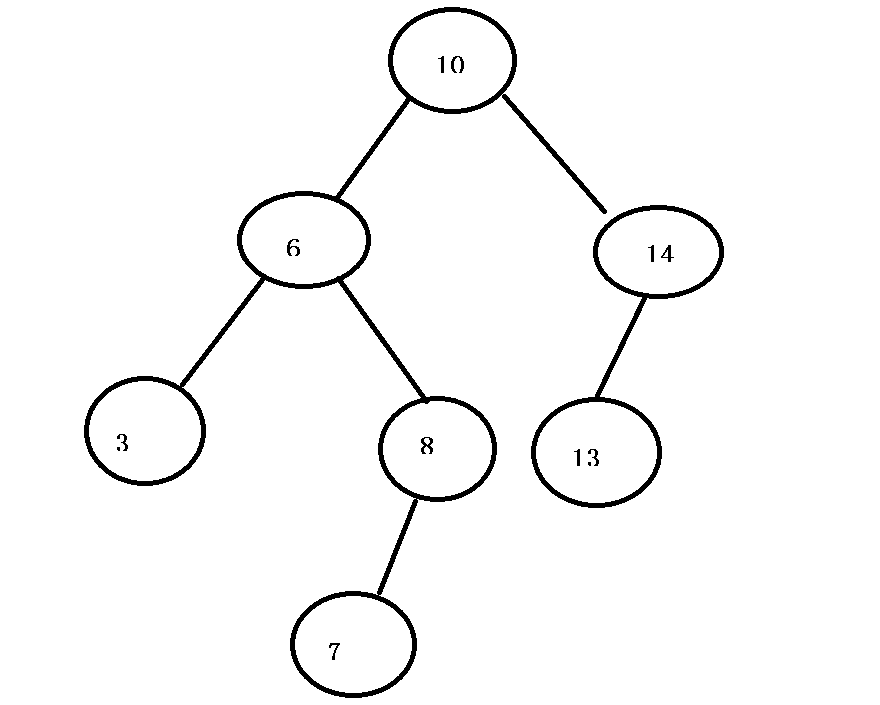
上图中就是一个二叉搜索树，如果要删除3和7这种叶节点就很好删除，直接删除然后将父节点的left或right置为空即可。

如果删的是8和14呢？此时它们的子节点就会遗留下来，要解决也很简单，采用“托孤”的方法，让要删除节点的父节点链接上删除节点的子节点即可。如要删除8，就让8的父节点6的right指向7即可。

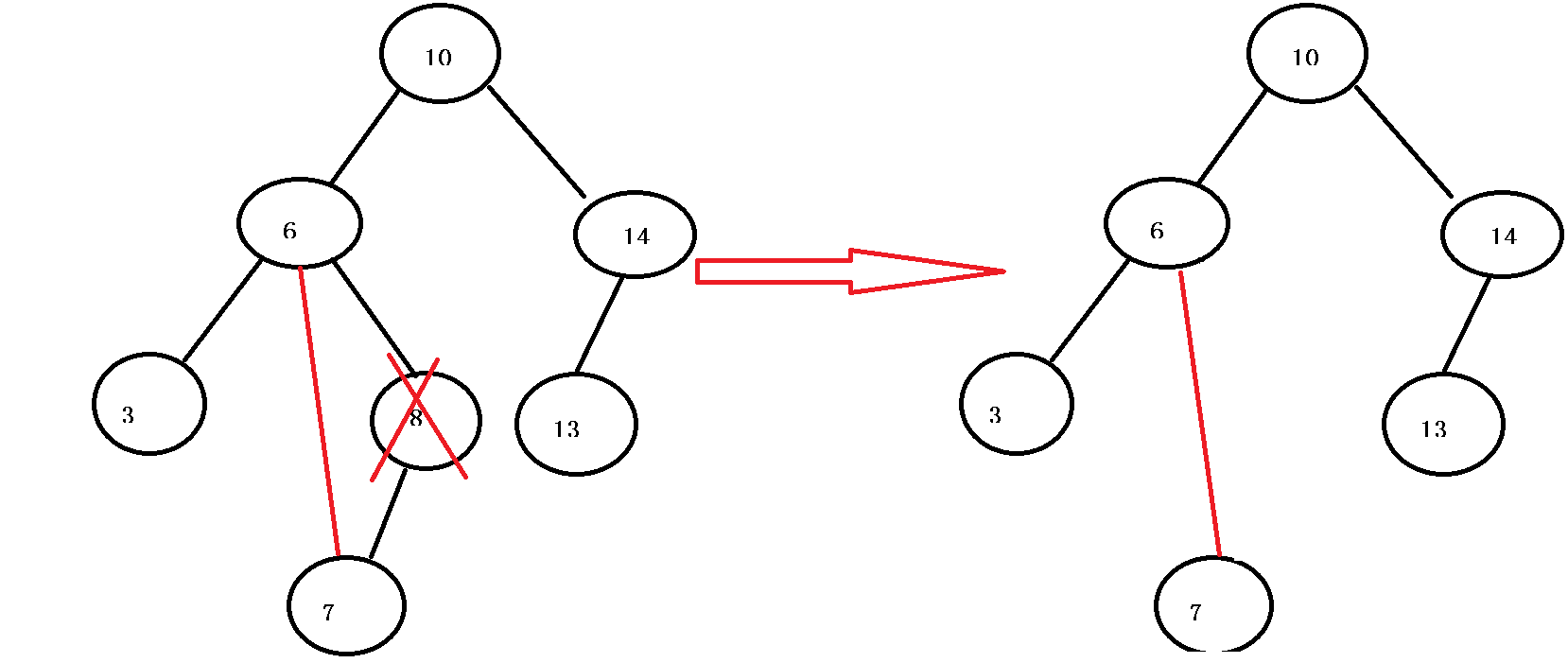
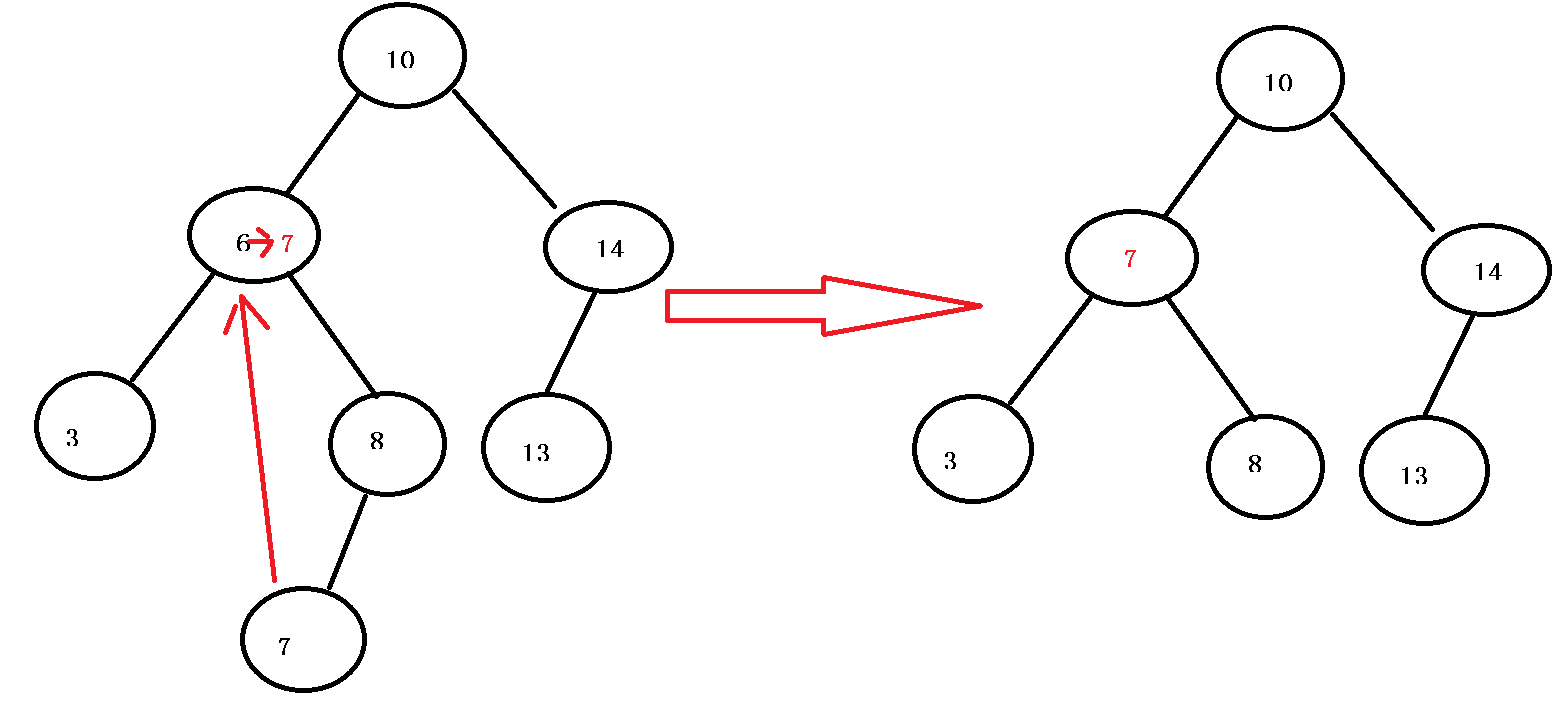
除了这种有一边为空或两边都为空的情况，还有一种情况就是它的子节点都不为空。如要删除6或者8。当遇到这种左右子节点都不为空的情况时，就可以采用“节点交换”的方法。例如如果要删除6，那么把6当做根节点，然后去找左子树的最大节点或找右子树的最小节点。这里以找右子树的最小节点为例，以6为根的右子树的最大子节点就是右子树的左子树的最小位置，在上图中就是7。找到后，将根节点赋值为最小节点的值，然后再将右子树的最小节点释放，再让父节点的left指向空即可。

其他几个函数的实现都不难，这里就不再一一讲解了。

三、二叉搜索树的两种模型

二叉搜索树其实有两种模型。第一种是“K模型”，第二种则是“KV模型”。

1. K模型

K模型，即只有key作为关键词，结构中只需要存储key即可。关键码即为需要搜索到的值。

例如，给一个单词word，判断该单词是否拼写正确。此时，就可以以词库中所有单词集合中的每个单词为key，构建一个二叉搜素树，然后用二叉搜索树检测该单词是否存在。

因为K模型以key为关键码搜索，所以K模型的二叉搜索树都是不允许随意修改和出现相同的关键码的。因此，在上面的模拟实现中，如果插入的值已经存在，就不会继续插入，而是返回false。

2. KV模型

KV模型，其每一个关键码key，都有与之对应的值value。即的键值配队。KV模型的二叉搜索树就很常见了。例如中英文转换，就可以看做是一种KV模型的二叉搜索树，以构成键值配对。再例如图书管理，在电子图书馆中，每一本书都是有自己的编号的，根据每本书的编号构建一棵二叉搜索树，在需要找书时，就可以根据编号去二叉搜索树中查找，效率就比一本一本的暴力查找高的多。

KV模型和K模型不同，是允许修改的。但是它所允许修改的值不是key值，而是Value值。也就是说，每个节点的关键码不能修改，但是关键码所对应的值可以修改。就如二叉搜索树中每一个节点存储的编号不能修改，但是可以修改这个编号所对应的书的名字。